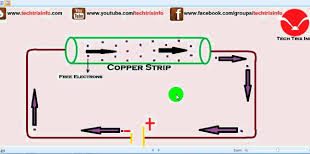
موقع المهندس موقع المهندس بيت كل مهندس من المعروف أن الموصلات مواد بداخلها شحنات حرة تتحرك حركة عشوائية غير منتظمة ولكنها تتحرك حركة منتظمة عند خضوعها لمجال كهربي في اتجاه معين مكونة ما يسمى بالتيار الكهربي . وهذه الشحنات الحرة عي الالكترونات في حالة الموصلات المعدنية , أما في حالة المواد السائلة والغازية فهي أيونات موجبة وسالبة .
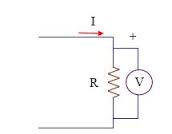
وتعرف شدة التيار الكهربي I بكمية الشجنة التي تمرخلال مقطع سلك في الثانية الواحدة فلو مرت شحنة مقدارها dq في زمن dt خلال مقطع السلك فإن شدة التيار تعطى ب
ووحدة التيار الأمبير ويساوي coulomb/sec , واتجاه التيار المصطلح هو عكس اتجاه تحرك الشحنات السالبة في الموصلات , وإذا أخذ اتجاه التيار وعلاقته باتجاه هذه الشحنات فإن المعادلة السابقة يمكن كتابتها على الشكل
(1)
وإذا تعرضت قطعة من سلك موصل منتظم الشكل لمجال كهربي شدته E ومتجه إلى اليسار فإن الالكترونات ستتحرك إلى اليمين فإذا فرض أن كل إلكترون يسير بسرعة ثابتة مقدارها v فإنه سيقطع مسافة مقدارها vdt في زمن قدره dt فإذا كانت مساحة مقطع السلك S وكانت n عدد الالكترونات في وحدة الحجم , فإن عدد الالكترونات التي تمر من مقطع السلك في زمن dt تساوي nsvdt فإذا كانت e تمثل شحنة الإلكترون , فإن الشحنة الكلية التي تمر في هذه المسافة في الزمن dt هي
dq=nevsdt
وتعرف كثافة التيار لموصل بأنها خارج قسمة التيار على مساحة المقطع للموصل أي أن
وتحدد هذه المعادلة متوسط كثافة التيار في المساحة s فإذا لم يكن التيار موزعا بانتظام فإنه يمكن اعتبار مرور التيار خلال مساحة متناهية في الصغر مقدارها ds وبذلك يمكن كتابة كثافة التيار بالصيغة التالية
(2)
أي أن كثافة التيار عبارة عن التيار حلال وحدة المساحة العمودية على اتجاه سريان الشحنة أما إذا كانت هناك زاوية بين J ومتجه الوحدة العمودي ds نجد أن
حيث يكون التكامل على السطح s وهذه هي العلاقة العامة التي تربط بين التيار وكثافة التيار , وحيث أن هي الكثافة الحجمية للشحنة فيمكن كتابتها على الصورة
وسبب تغيير التفاضل الكلي إلى تفاضل جزئي هو أن الكثافة الشحنية تابعة لكل من الزمان والمكان وفي هذه الحالة هي تابعة للزمن فقط , وإذا أخذنا حجما V محاطا بسطح ثابت S, فإن التيار يمثل التغير في الشحنة بالنسبة للحجم V عبر مقطع المساحة S وحسب قانون حفظ الشحنة فإن معدل نقصان الشحنة داخل حجم ما يساوي التيار الكلي المتدفق خارج السطح المحيط بالحجم , وبالتعويض في 1 عن 4 و 3
(5)
وباستخدام نظرية جرين نحصل على
(6)
وحيث أن المعادلة صحيحة لأي حجم
وتعرف هذه المعادلة بمعادلة الاستمرارية للتيار الكهربي وكثافة التيار.
